Hold up a finger and look at it with just one eye, then switch to just the other and you'll see your finger appear to ‘jump’ from side to side.
The further away the finger, the smaller the jump.
This apparent shift of a nearby object against a distant background when observed from different positions is called parallax.
Measuring the size of this 'jump' as an angle is the same technique astronomers traditionally used to find the distances to celestial objects such as stars.
Our DIY project is an instrument to demonstrate the principle, and is known as a parallax measuring tool.
Extra materials to help with the build
Download our Parallax Distance Calculator (Excel)
Download our Parallax Calculator Diagram (PDF)
Using the parallax measuring tool
Our parallax instrument includes a long base stick with an observation point at either end.
When we look at a nearby object (we used a green tennis ball) from each point, we use the built-in protractors to measure the apparent shift of the object either side of a reference point in the distance (in our case, a yellow star on a fence).
The sum of these angles is the apparent shift of our nearby object.
Using our instrument and some parallax maths (see links in Extra Materials above) we calculated the distance to the ball to be 8.3 metres.
The true distance was 7.6 metres, which is quite close. If we had placed the star further away, it would have been more accurate!
Our instrument uses degrees as the unit for angles, but when measuring nearby stars the angles involved are too small to sensibly record this way.
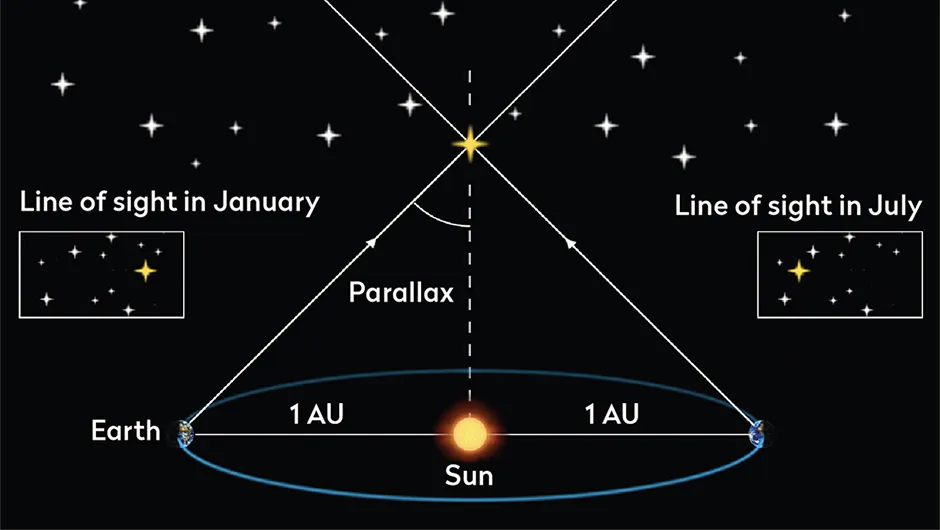
How astronomers measure parallax
Astronomers therefore use arcseconds, where 3,600 arcsecond = 1 degree.
They also use a longer base distance.
The largest base distance on Earth is achieved by waiting six months to take measurements when Earth is at the two furthest points from the Sun in its orbit, giving a base distance of 2 astronomical units (AU).
This is how the distances to nearby stars have traditionally been determined. Instead of using protractors, modern methods involve counting pixels on a digital image.
A star’s parallax angle is the angle made with a base line of 1 AU; therefore the observed shift six months apart is divided by two.
Our nearest star (after the Sun) is Proxima Centauri.
This has the largest parallax angle of 0.7685 arcseconds. If an imaginary star had a parallax angle of 1 arcsecond, its distance would be 1 parsec.
The distance to Proxima Centauri is therefore 1.3 parsecs.
Traditional Earth-based parallax methods measure distances up to about 30 parsecs, but radioastronomy, photometry and satellite imaging now make it possible to measure parallax angles to far greater distances and to an accuracy of 10 millionths of an arcsecond!
Equipment
- One base stick, approximately 2 metres x 34mm x 18mm
- Two pieces of good-quality plywood, approximately 120mm x 120mm x 15mm
- Two short offcuts of softwood, approximately 50mm x 34mm x 34mm
- Two cheap 360⁰ angle-measuring protractors
- Two straws to use as viewing tubes
- Six short woodscrews with washers; four 30mm screws to attach to the base stick
- One 1/4-inch x 20TPI nut (if using this method to mount to a tripod)
- Drill, bits, countersink bit, screwdriver
- Marking-out tools, hot glue gun, paint
Step-by-step
Step 1

Find the centre of each plywood square by drawing diagonals. Draw around the protractor and mark the position of the three mounting screw pilot holes (just outside the circumference). Finally, mark the two screw holes for attaching to the base stick.
Step 2

Drill three 2mm pilot holes and two 4.5mm clearance holes to mount the plywood to the base stick. Countersink these holes using a countersink drill bit (or, if you don't have one, a large drill bit), so that the screws finish flush with the surface.
Step 3

Take your offcut blocks and drill a large hole in the bottom of each so that they fit over the central ‘knobs’ of the protractors. Drill a horizontal hole through each block for the straw to pass through. Sand all of the wooden parts smooth and paint them.
Step 4

Use three screws with washers to hold each protractor to its plywood square. Tighten the screws just enough that it holds but still allows the whole protractor to turn when setting up the experiment. Push a viewing straw through each block.
Step 5

Glue a block to each protractor. Make sure that the straw is aligned with the pointer arm. Screw the plywood squares to either end of the long base stick. Glue a 1/4-inch x 20TPI nut under the centre of the stick for mounting to a tripod (optional).
Step 6

Set the instrument, object (ball) and distant object (star) at similar heights. Set each protractor to zero. Point the straws at the stars. Turn just the arm of each protractor to point at the object. Read off the two small angles. Use our calculator at the top of this article to find the distance.
Have you built our parallax measuring tool? Let us know by emailing contactus@skyatnightmagazine.com










