Starting on 15 April, in this guide we'll show you how to track the discrepancy between mean and apparent solar times by marking where a gnomon’s shadow falls at the same time each day.
A sundial is an easy way to measure time. You simply put a stick in the ground and mark where the end of the stick’s shadow falls on the hour.
Not too much of a challenge you might think, but there are hidden details you need to consider.
- Follow our DIY project to make your own portable sundial

The trouble is, the sundial’s measured daily time starts to drift with respect to clock time.
Time will not always be shown accurately, a small difference at first, then larger, then smaller, then zero and so on.
The problem isn’t with your sundial, it’s with the Sun, or rather with Earth. Earth’s orbit about the Sun isn’t a circle, it’s an ellipse.
As Earth orbits the Sun, the elliptical orbit causes the Earth–Sun distance and our orbital speed to alter.
For us sitting on the surface of our planet, the apparent speed of the Sun across the sky appears to speed up and slow down in a periodic manner.
We can’t gauge time properly using this variable Sun, known as the real or apparent Sun, so we create an imaginary one that moves across the sky at a consistent rate: the mean Sun.
When to measure the equation of time
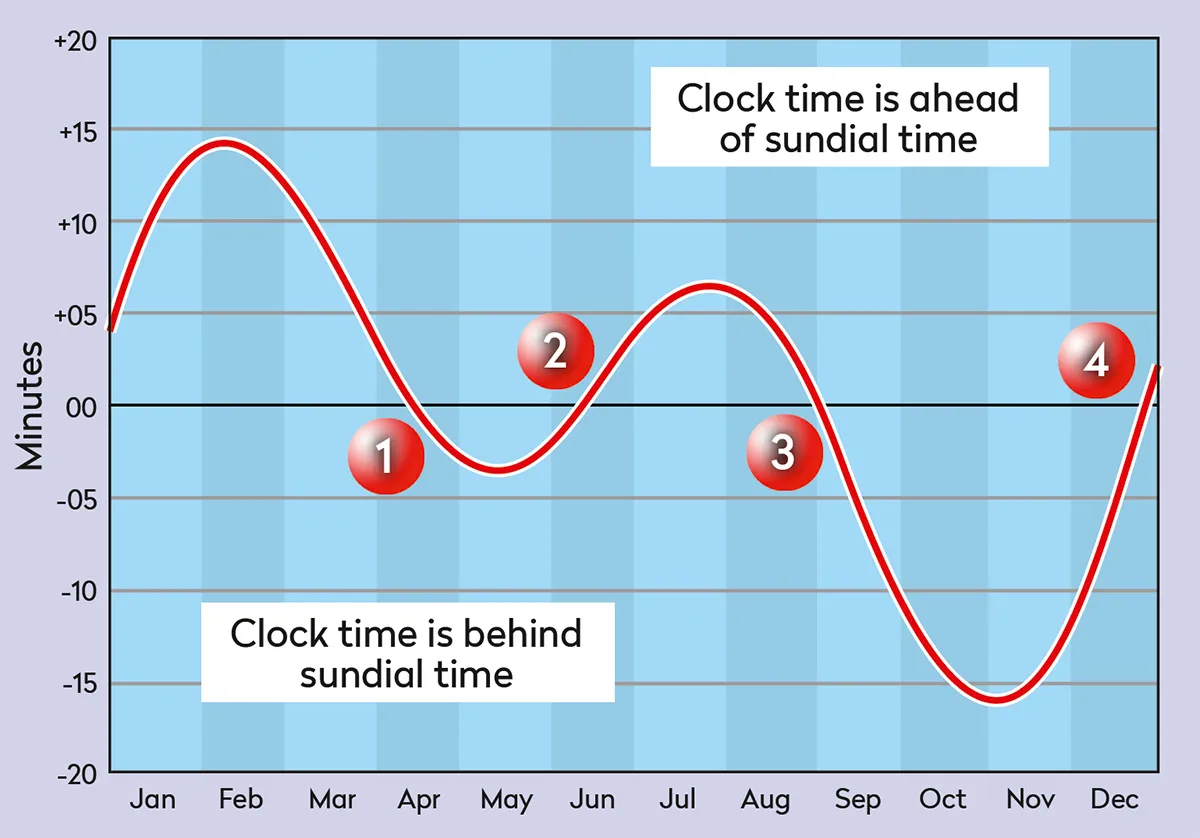
The mean and apparent Sun align on four dates throughout the year: on 15 April, then 13 June, 1 September and 25 December (correct for J2000.0).
At such times, the end of the shadow of our sundial stick (gnomon) marks the correct time. On other days the mean Sun is either ahead of or behind the apparent Sun.
The difference is known by the rather enigmatic name of ‘the equation of time’ and can range from 14 minutes and 15 seconds ahead of clock time to 16 minutes and 25 seconds behind.
The variation can be demonstrated to great effect by photographing the position of the Sun over the course of a year at the same UT time.
If you do this, the equation of time causes it to oscillate back and forth. However, Earth’s axial tilt also plays a part, causing the Sun to appear to move up and down in the sky over the course of a year.
As a consequence, the equation of time plus declination drift produces a bowling pin shape in the sky, known as an analemic curve.
Marking the position of a gnomon’s shadow tip at the same time of day throughout the year will also produce this curve, and that’s your challenge for the rest of 2023 and into 2024!
This requires good placement of the gnomon so it’ll be in Sun throughout the year.
It also requires good weather. Don’t worry about missing days though – the shape can still be revealed, even with many gaps.
This guide originally appeared in the April 2023 issue of BBC Sky at Night Magazine.
