If space is infinite, how can we say it's curved or flat?
Things can be curved. That’s an uncontroversial statement. I’m thinking of things like sheets of paper, metal rods or the surface of Earth.
You can look at these things and judge whether they are curved or flat for yourself.
It also seems fairly uncontroversial to say that empty space isn’t a thing: it’s just the gap between things.
That makes the idea of curved space sound ludicrous.
But you’ve almost certainly heard the phrase uttered in connection with the theories of Albert Einstein. So, what does it mean? How can something that’s not there be curved?
Read more:
- How do we measure distance in space?
- When we look at the night sky, how far back in time can we see?
- What happened during the first seconds of the Universe?

You might wonder whether this is some special technical use of the word ‘curved’, or just a metaphor to suggest it’s like a curved thing.
No. You are genuinely being asked to believe that the vacuum – the void in between things in space – can itself be bent.
The correct response to this idea is, "Huh? What the...?", and that’s a fair question.
It would also be fair to ask, "Never mind it being curved. How can space – emptiness, nothingness – have any properties at all?" Let’s start with that question before we tackle the biggie.
Is space empty?
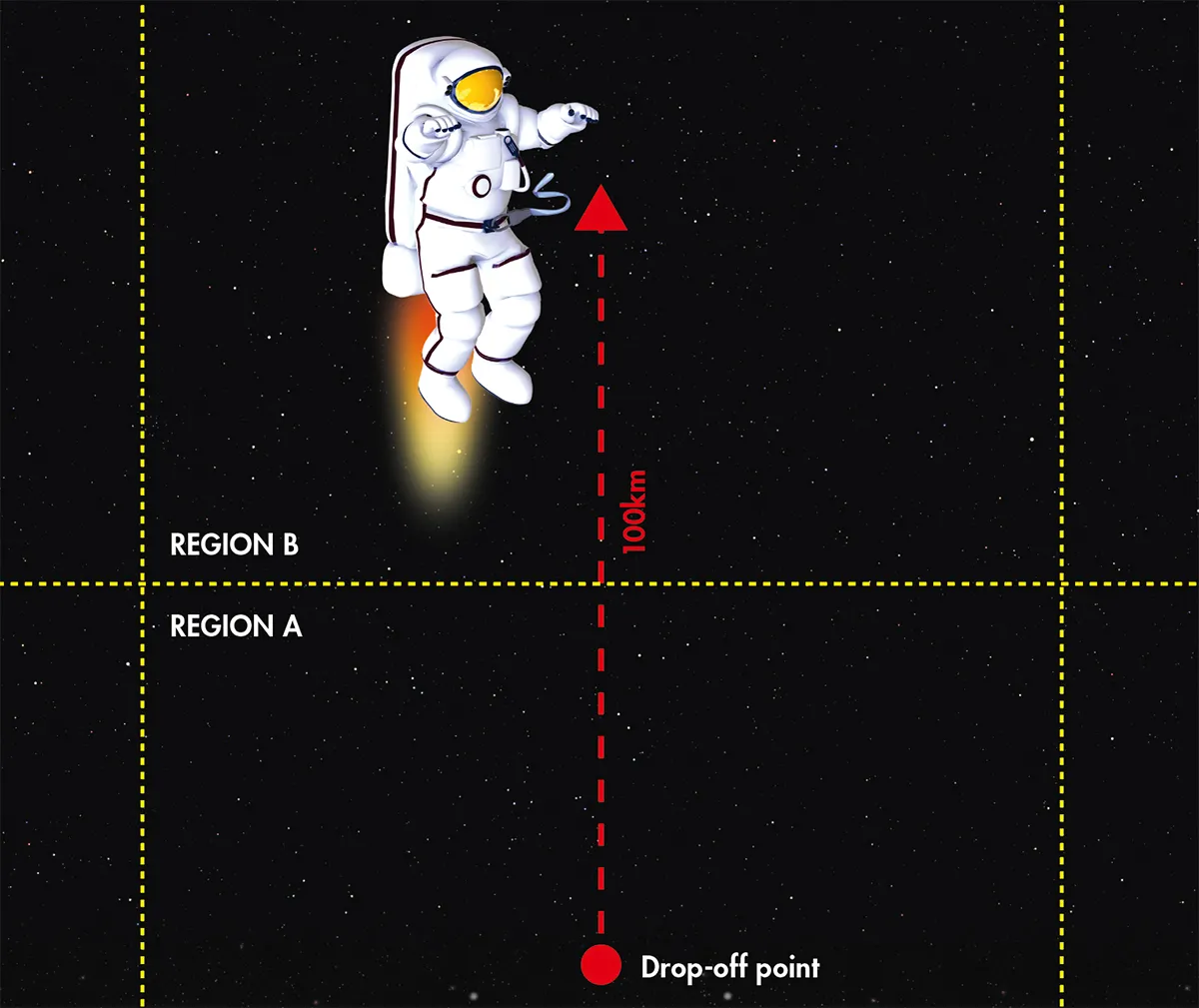
You find yourself floating in space You activate your spacesuit’s jet pack and head out 100km forwards from the drop-off point.
Knowing that you were initially stationary with respect to Earth and using an accelerometer (like the one in a smartphone) to keep track of any changes in speed, you can work out how far you have gone just by measuring the time since you set out.
After 100km, you decide to turn around and return to the drop-off point. You know that, if you travel 100km back the way you came, you’ll be back at the drop-off point. But how do you know that’s the case?
Take a look at the illustration above. Well, the bit of space you’re now in, Region B, is still connected to Region A, where you started, because those parts of space were joined together a moment ago during the outward journey.
You confidently expect them still to be joined together.
Given that, it’s not so strange to believe that space possesses some properties of it own.
In fact, we rely on it having the property of connectivity – that each bit of space ‘remembers’ which other bits are its neighbours, so that when you retrace your path, you get back to where you started, because the space is still connected up in the same way.
But what if you don’t turn back after the first 100km? Instead you make a 90º left turn, travel another 100km, turn left 90º again, then travel another 100km – so you’re moving parallel to your first path as in the illustration below.
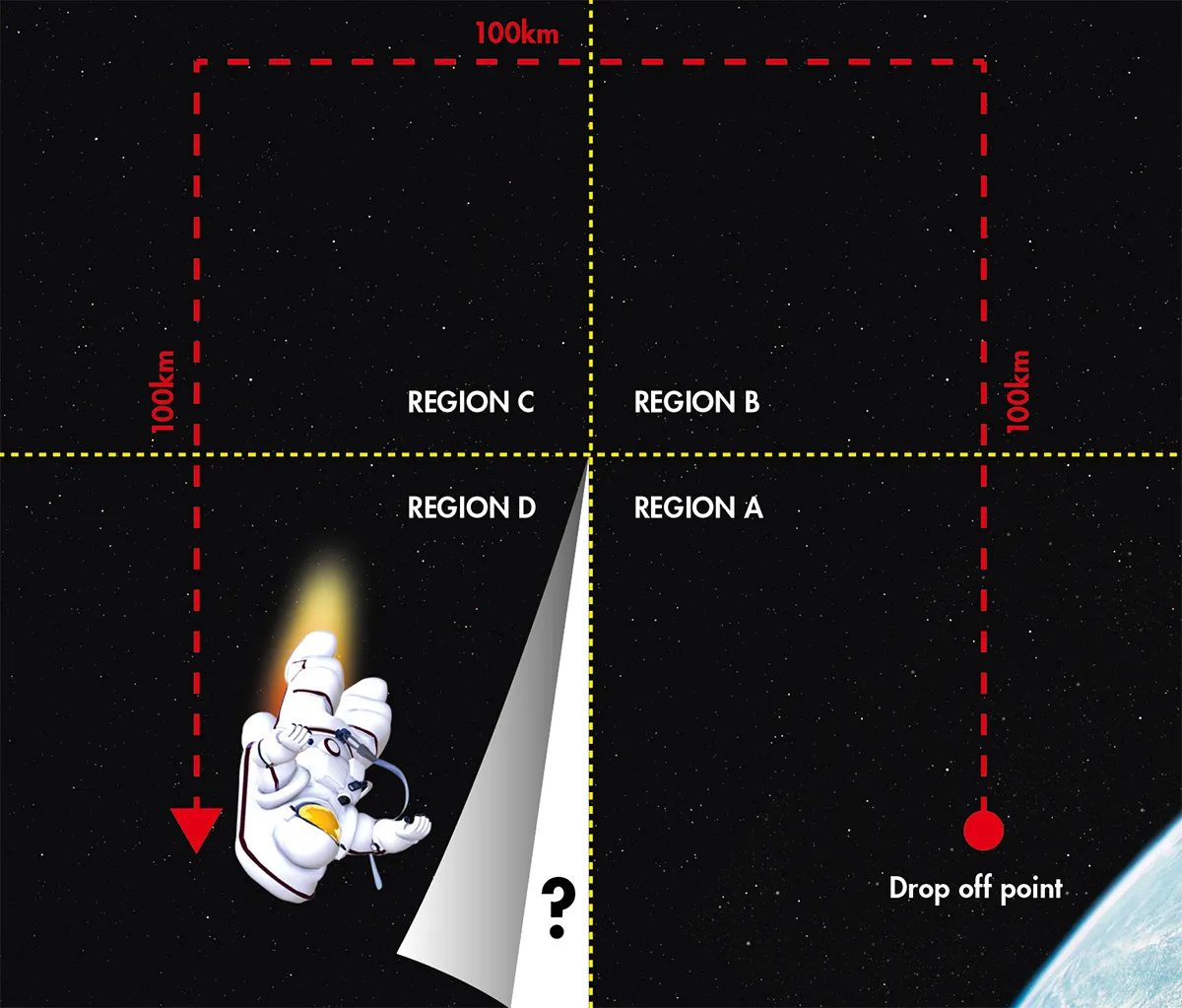
You’ve followed three sides of a square, so now you must be 100km from the rendezvous, right?
Again, this seems obvious, but is it? If you followed the same journey around New York’s famous grid of roads you could be confident of your location, because you know how the roads join up.
But we’re talking about travelling through dark, empty nothingness. Can we rely on regions of space joining up in a well-behaved manner like Manhattan’s streets?
As seasoned readers will know, the Universe is rarely well-behaved, but always entertaining.
Here on Earth, where space is relatively simple, every time that I have followed a square path it has so far taken me back to my starting point.
So I have come to expect it. But it doesn’t have to be that way. And, in many parts of the Universe, it isn’t.
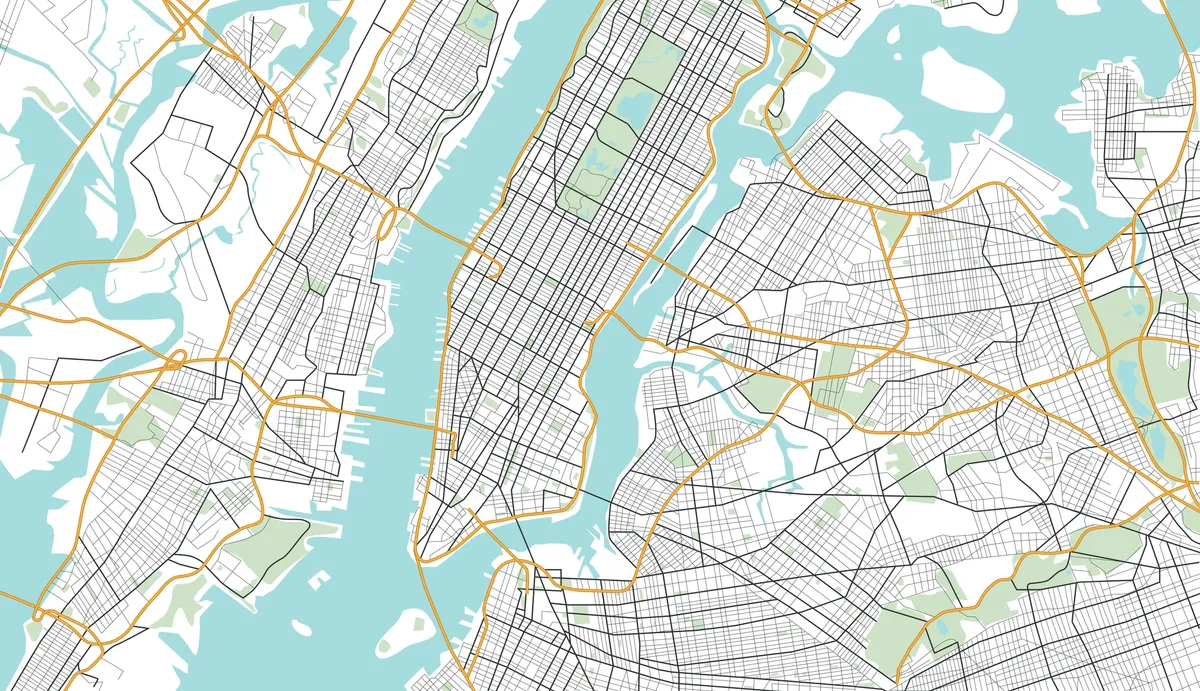
Don’t worry, the story of your inaugural spacewalk has a happy ending because, in our local neighbourhood of space, any 100km square joins up almost perfectly.
But to navigate enormous distances, comparable to the size of the Universe, or even modest distances near a black hole, you cannot follow a square-grid-shaped map like the one pictured, because the regions of space don’t join up like that.
Now we’re ready to define what is meant by ‘curved space’.
If the regions of space meet each other in the straightforward way, so that an astronaut can follow a square or circular route and come back to the beginning after turning through a total of 360º, then we call that region of space ‘flat’.
On the other hand, if the lengths along different parts of the path don’t agree with each other, then the space is called ‘curved’.
In fact, it’s not just called curved, it’s curved in a very real sense. To see why, we must imagine what life would be like for a ‘Flatlander’ living in a 2D universe.
Measuring a curved object
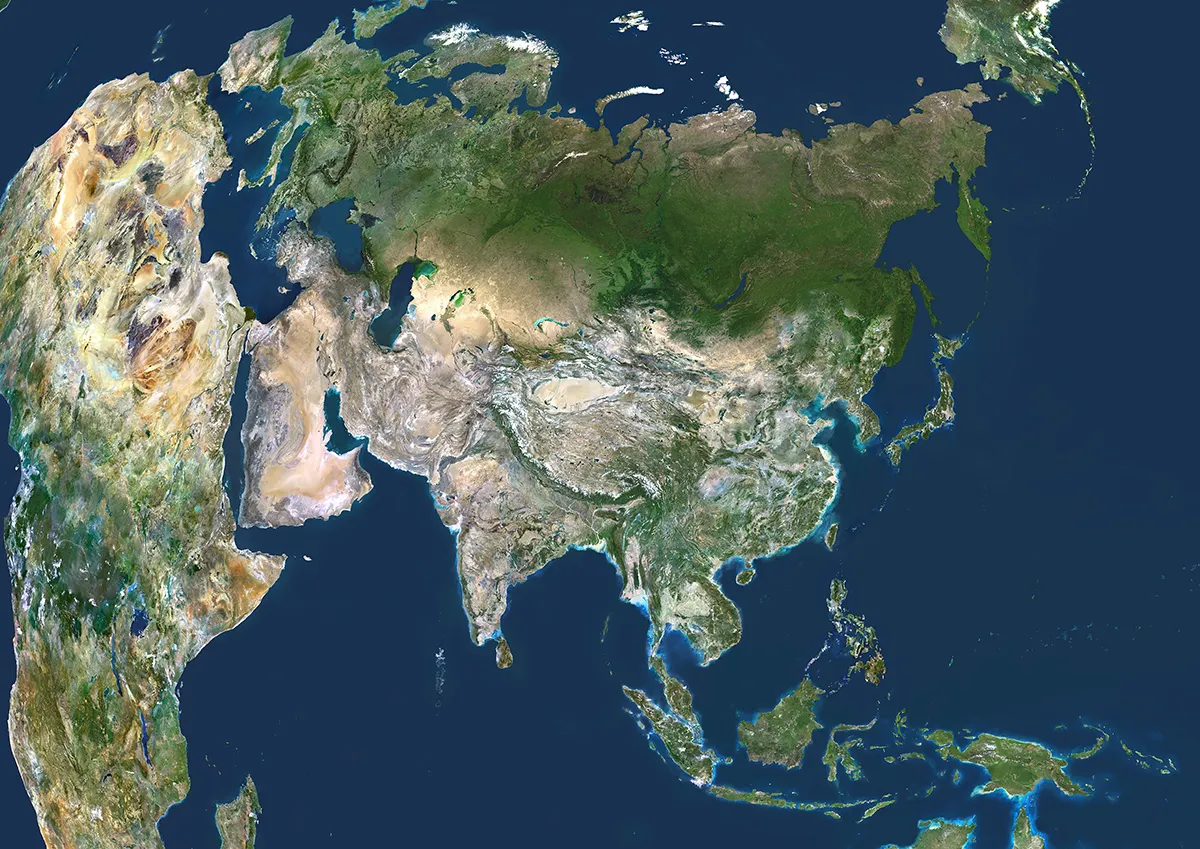
As early cartographers discovered, it’s impossible to map Earth’s surface in 2D using a simple square grid, because the surface of our planet is curved.
Remember, curvature is the property where the parts of the surface don’t join together like a square grid.
This definition makes sense even if, like Flatlanders, you cannot reach a vantage-point outside your curved space to get a good look at its shape.
Flatlanders, who cannot rise above their curved universe to view its spherical shape, can still work out that their universe is curved by drawing a grid all over it and seeing how the shapes fit together.
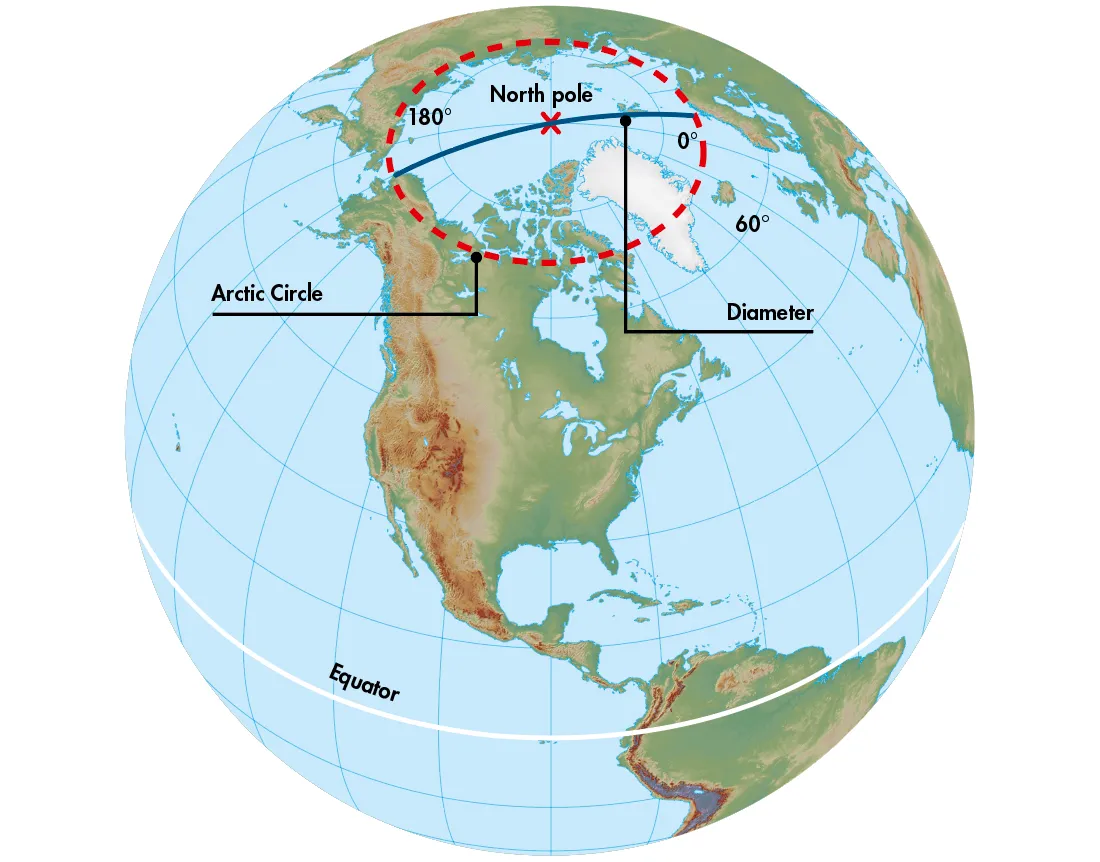
Another way that you can measure the curvature of a sphere (like Earth’s surface) without ever leaving it is to draw a big circle on it – for instance, the Arctic Circle – and measure its circumference.

Next measure its diameter. You’re not allowed to leave the surface by drilling a tunnel through the Earth to measure a straight-line path; you have to trek across the Arctic, unravelling a tape measure, to find the diameter across the surface.
Having obtained these two measurements, divide the Arctic Circle’s circumference by its diameter.
Time to revisit a bit of high school maths: dividing the circumference of a circle by its diameter should always give you π (3.14159265358979 and a bit).
But this isn’t the figure you end up with. The Arctic isn’t flat, it’s curved. It has a circumference that is too short for its diameter and this discrepancy tells you how curved the surface is.
So far, we have been talking about a simple curved surface, to see how a Flatlander could measure the curvature of their 2D universe without ever leaving it.
Now let’s talk about the 3D space that we live in, which physicists claim is curved.
Like the Flatlanders, we cannot leave our Universe to get a good look at its shape from the ‘outside’.
In truth, there is no outside.The Universe doesn’t need a bigger space around it to curve into.
Trapped as we are within the 3D space, we can still measure its curvature by seeing if the rules of simple geometry go wrong.
One way of doing this is measuring the surface area of a big sphere (the 3D version of measuring the circumference of the Arctic Circle) and comparing it with the sphere’s diameter.
If the 3D space enclosed by the sphere is curved, then the sphere’s surface will be either too big or too small compared with its diameter.
But does that ever really happen? Einstein predicted that it does. According to his theory of gravity, every object in the Universe makes the space around it curve to a greater or lesser extent.
How gravity curves space

In his general theory of relativity, Albert Einstein proposed that space gets curved by massive objects and that this causes gravity.
Isaac Newton had explained that objects (apples, billiard balls, etc) either stay still or move in straight lines when no force is acting on them.
So when an object moves in a curve, like the Moon’s elliptical orbit around Earth, it shows that a force is at play – in that case, Earth’s gravity pulling on the Moon.
Einstein’s theory says that, in a sense, there is no force acting on the Moon, so it actually travels in a straight line through space, but the space (strictly, the spacetime) that it’s moving through is curved.

So curvature of space has the same effect as a force and that’s what gravity is.
Because space is curved, even light rays must be deflected by gravity.
A heavy object like a galaxy can distort light rays so much that it alters the images of objects beyond it, like a lens. This phenomenon is known as gravitational lensing.
In rare cases where two such galaxies are perfectly aligned with the Earth, the background galaxy appears spread out in a ring around the foreground object.
These ‘Einstein rings’, like the one shown above, are extremely useful as they allow astronomers to work out exactly how curved the ‘lens’ is and thus accurately weigh the foreground galaxy, complete with its halo of dark matter.
This article originally appeared in the December 2021 issue of BBC Sky at Night Magazine.

